Data Structures — Binary Tree

A Binary Tree is a hierarchical data structure consisting of nodes, where each node can have up to two children, commonly known as the left child and the right child. In this article, I explore the fundamental concepts of a Binary Tree and demonstrate the main traversal strategies using code examples in .NET.
Binary Tree
These are some important terms related to a Binary Tree:
- Node: it represents a termination point in a tree.
- Root node: it is the top node of the Binary Tree.
- Branch: it refers to the connection or path between nodes within the tree structure, it represents the relationship between a parent node and its child node(s). It is also used the terms “root branch” for the topmost node of the tree, “left branch” for a branch that connects a parent node to its left child node, and “right branch” for a branch that connects the a parent node to its right child node.
- Parent node: it is a node (except the root) in a tree that has at least one node.
- Child node: it is a node that is connected to a node above it.
- Leaf node: it is a node that has no children, and is located at the bottom level of the tree.
- Internal node: it is a node that has at least one child.
- Depth: it is the number of edges on the longest path from the root node to that node.
- Height: it is the length of the longest path from the root node to a leaf node.
Node
In a binary tree, a node is a block that represents a single element of data within the tree. Each node contains two main components:
- Data: which can be of any type (i.e.: integer, a string, an object, etc).
- References to Children: each node in a binary tree can have at most two children: a left child and a right child. Nodes are connected to each other through these references, forming the hierarchical structure of the binary tree.
A Binary Tree has these three characteristics:
- Has exactly one root.
- Each node has at most two children.
- Has only one path (a connection) between the root and any node.
Binary Tree Example
Below you can see a graphical representation of a Binary Tree. This is an example of a binary tree, but the tree could be bigger or smaller:

- Node 1 is the root node.
- Node 1 contains 2 children: node 2 (left node) and node 5 (right node).
- Node 2 contains two children: node 3 (left node) and node 4 (right node).
- Node 5 contains only one child: node 6 (right node).
- Nodes 3, 4 and 6 are the leaf nodes.
TreeNode
This is a representation of a TreeNode class in C#:
public class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val = 0, TreeNode left = null, TreeNode right = null) {
this.val = val;
this.left = left;
this.right = right;
}
}For demonstration purposes, I’m creating the following Binary Tree, which will be used in the next examples:
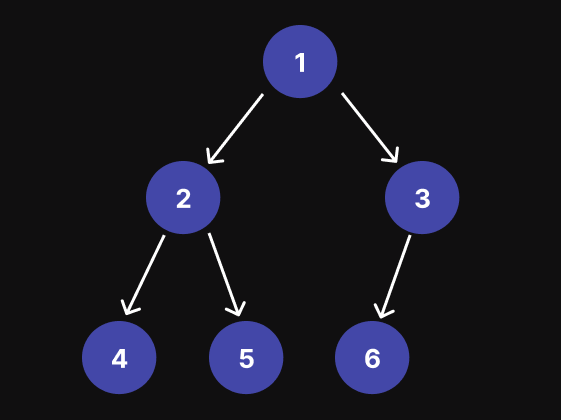
// Tree with nodes [1, 2, 3, 4, 5, 6, null]
// 1
// / \
// 2 3
// / \ /
// 4 5 6
static TreeNode CreateDemoTree()
{
return new TreeNode(1)
{
left = new TreeNode(2)
{
left = new TreeNode(4),
right = new TreeNode(5)
},
right = new TreeNode(3)
{
left = new TreeNode(6)
}
};
}With this class, now let’s dive in on how we can iterate over a Binary Tree. These are well-known algorithms that can be used to iterative over the Binary Tree, and I’m going to explain them step by step.
Tree Traversal Algorithms
A traversal strategy is a method or technique used to visit all the nodes in a data structure (such as a tree or graph) in a specific order. In the context of binary trees, traversal strategies determine the sequence in which nodes are accessed and processed. Traversal strategies are crucial for various applications, including data searching, manipulation, and structure validation.
There are two general strategies that can be used to traverse a tree:
- Depth-First Search (DFS): in this strategy, we adopt
depthas the priority, so that one would start from a root and reach all the way down to a certain leaf, and then back to root to reach another branch. The DFS can be used to perform thePreorder,Inorder, andPostordertraversal. DFS uses a stack data structure (explicitly or implicitly via recursion) to keep track of the nodes visited and the traversal order. - Breadth-First Search (BFS): in this strategy, we scan through the tree level by level, following the order of height, from top to bottom. The nodes on higher levels would be visited before the ones with lower levels. This strategy explores all neighbours of a node before moving to the next level of nodes. The BFS can be used to perform
Level OrderandReverse Level Ordertraversal. BFS uses a queue to maintain the order of nodes to be visited.
If you want to know how a Stack or a Queue works, check my articles:
- Data Structures — Stack
- Data Structures — Queue
Five common approaches used for exploring and processing the nodes of a binary tree are:
- Preorder Traversal: traverse the entire binary tree in the following order:
Root -> Left -> Right. - Inorder Traversal: traverse the entire binary tree in the following order:
Left -> Root -> Right. - Postorder Traversal: traverse the entire binary tree in the following order:
Left -> Right -> Root. - Level Order Traversal: traverse the entire binary tree per level, from
Top to Bottomand fromLeft -> Right, level by level. - Reverse Level Order Traversal: traverses the entire binary tree from
Bottom to Topand fromRight -> Leftat each level (storing the results in reverse order).
Three common ways to perform a Tree Traversal are:
- Recursive Approach: in this approach, we use recursion to perform the traversal. For that, we create a helper function to recursively traverse the binary tree. It initializes an empty list to store the result of the traversal and then calls the helper function, passing the root of the binary tree and the result list as parameters.
- Iterating over the tree using a Stack: in this approach, a Stack is used to simulate the recursion process and to iteratively traverse the binary tree. It initializes an empty list to store the result of the traversal, and a stack to keep track of nodes that need to be processed.
- Morris Traversal Approach: in this approach, we traverse the tree without using a stack or recursion, by establishing and removing temporary links within the binary tree.
I’m going to present each of these approaches next.
Preorder Traversal (DFS)
The Preorder Traversal is a tree traversal algorithm used to visit each node in a binary tree systematically. It receives this name because the root node is visited before its children nodes. In this approach, you traverse the entire binary tree in the “Root -> Left -> Right” order.
The nodes are visited in the following order:
- First, visit the Root node of the tree and process its value.
- Then visit the Left subtree (move to the left subtree of the current node).
- Then visit the Right subtree (after visiting all nodes in the left subtree)
For example, for the binary three in the image below, the result of the Preorder Traversal is: [1, 2, 4, 5, 3, 6]:

Recursive Approach
In the Recursive Approach for Preorder Traversal, we visit each node starting from the root node, then recursively visit the left subtree, and finally recursively visit the right subtree:
public static IList<int> RecursiveApproach(TreeNode root)
{
List<int> result = new List<int>();
// Call the helper function to perform the preorder traversal recursively
Preorder(root, result);
return result;
}
// Helper method that performs the traversal
private static void Preorder(TreeNode node, List<int> result)
{
if (node == null) return;
// Visit the current node (root) and add its value to the result list
result.Add(node.val);
// Recursively traverse the left subtree
Preorder(node.left, result);
// Recursively traverse the right subtree
Preorder(node.right, result);
}Iterative Approach using a Stack
In this approach, we start from the root and then at each iteration, pop the current node out of the stack and visit this node. Then if this node has a right child we push its right child into the stack, and if this node has a left child we push its left child into the stack (we push the right child first so that we can visit the left child first since the nature of the stack is LIFO — Last In First Out), after that we can continue the next iteration until the stack is empty. In this approach, we push nodes into the output list following the order Top-Bottom and Left -> Right, which naturally reproduces preorder traversal:
public static IList<int> IterativeApproach(TreeNode root)
{
// Initialize a stack to store nodes that need to be processed
var stack = new Stack<TreeNode>();
// Initialize a list to store the preorder traversal result
var output = new List<int>();
if (root == null)
{
return output;
}
stack.Push(root);
while (stack.Count > 0)
{
// Get the current element in the stack
TreeNode node = stack.Pop();
// Add the value of the popped node to the output list
output.Add(node.val);
// If the popped node has a right child, push it onto the stack
if (node.right != null)
{
stack.Push(node.right);
}
// If the popped node has a left child, push it onto the stack
if (node.left != null)
{
stack.Push(node.left);
}
}
// Return the output list containing the preorder traversal of the tree
return output;
}Morris Traversal Approach
In this approach, the traversal starts at the root and follows these steps: for each node, if it has no left child, its value is added to the output, and it proceeds to the right child. If the node has a left child, it finds the rightmost node in the left subtree (predecessor). If the predecessor’s right child is null, the algorithm creates a pseudo-link back to the current node and moves to the left child. If the predecessor already points to the current node, the link is removed, and the traversal moves to the right child. This method effectively traverses the tree in order while avoiding extra memory use, with pseudo-links serving as a temporary breadcrumb trail for navigation.
public static IList<int> MorrisTraversalApproach(TreeNode root)
{
var output = new List<int>();
TreeNode node = root;
// Traverse the tree until we reach the end
while (node != null)
{
// If the current node has no left child
if (node.left == null)
{
// Add the value of the current node to the output list
output.Add(node.val);
// Move to the right child of the current node
node = node.right;
}
else
{
// If the current node has a left child
// Find the predecessor of the current node
TreeNode predecessor = node.left;
while (predecessor.right != null && predecessor.right != node)
{
predecessor = predecessor.right;
}
// If the predecessor's right child is null, link it to the current node and move to the left child
if (predecessor.right == null)
{
// Add the value of the current node to the output list
output.Add(node.val);
// Link the predecessor's right child to the current node
predecessor.right = node;
// Move to the left child
node = node.left;
}
else
{
// If the predecessor's right child is not null, unlink it and move to the right child
// Unlink the predecessor's right child
predecessor.right = null;
// Move to the right child
node = node.right;
}
}
}
// Return the preorder traversal output
return output;
}Inorder Traversal (DFS)
The Inorder Traversal is a tree traversal algorithm used to visit each node in a binary tree systematically. In this approach, you traverse the entire binary tree in the “Left-Root-Right” order.
The nodes are visited in the following order:
- First, visit the Left subtree, by starting at the Root node and moving to the left child of the current node, if it exists. Repeat this process until reaching a node with no left child.
- Then visit the Right subtree, by moving to its right child, if it exists. Repeat the traversal process for the right subtree.
- Then repeat these steps for each node in the binary tree until all nodes have been visited.
In summary, we first visit the left subtree, then the root node, and then the right subtree. For example, for the binary three in the image below, the result of the Inorder Traversal is: [4, 2, 5, 1, 6, 3]:

Recursive Approach
In the Recursive Approach for inorder traversal, we start by checking if the current node is not null, and if so, it recursively traverses the left subtree, adds the value of the current node to the output list, and then recursively traverses the right subtree.
This process continues until all nodes in the binary tree are visited. As a result, the result list contains the elements of the binary tree in sorted order, representing the inorder traversal.
public static IList<int> RecursiveApproach(TreeNode root)
{
// Initialize a list to store the inorder traversal result
var result = new List<int>();
// Call the helper function to perform the inorder traversal recursively
Inorder(root, result);
// Return the list containing the inorder traversal result
return result;
}
// Helper method that performs the traversal
private static void Inorder(TreeNode root, List<int> output)
{
// Base case: If the current node is not null
if (root != null)
{
// Traverse the left subtree of the current node recursively
Inorder(root.left, output);
// Add the value of the current node to the output list
output.Add(root.val);
// Traverse the right subtree of the current node recursively
Inorder(root.right, output);
}
}Iterative Approach using a Stack
In this approach, we start with the current node set to the root of the binary tree, the code enters a loop that continues until either the current node becomes null and the stack becomes empty, indicating that all nodes have been processed.
Within the loop, it traverses the left subtree of the current node by repeatedly pushing each node onto the stack and moving to its left child node. Once the left subtree traversal is complete, it pops a node from the stack, adds its value to the result list, and moves to its right child node to continue the inorder traversal. Finally, after completing the traversal, the code returns the list containing the inorder traversal result.
public static IList<int> IterativeApproach(TreeNode root)
{
// Initialize a list to store the inorder traversal result
List<int> result = new List<int>();
// Initialize a stack to store nodes that need to be processed
Stack<TreeNode> stack = new Stack<TreeNode>();
// Start with the current node set to the root of the binary tree
TreeNode curr = root;
// Continue the loop until either the current node becomes null
// and the stack becomes empty, indicating that all nodes have been processed
while (curr != null || stack.Count > 0)
{
// Traverse the left subtree of the current node
while (curr != null)
{
// Push each node onto the stack
stack.Push(curr);
// Move to the left child node
curr = curr.left;
}
// Once the left subtree traversal is complete, pop a node from the stack
// This node will be the current node whose value needs to be added to the result list
curr = stack.Pop();
// Add the value of the current node to the result list
result.Add(curr.val);
// Move to the right child node to continue the inorder traversal
curr = curr.right;
}
// Once the traversal is complete, return the list containing the inorder traversal result
return result;
}Morris Traversal Approach
In this approach, we initialize an empty list res to store the inorder traversal result and sets the current node pointer curr to the root of the binary tree. Within a loop that continues until the current node becomes null, the code checks if the current node has a left child. If it does, it finds the rightmost node in the left subtree (predecessor node) and makes the current node the right child of the predecessor.
It then stores the current node, moves to its left child, and sets the left child of the original current node to null to prevent infinite loops. If the current node has no left child, its value is added to the result list, and the current node moves to its right child. Finally, after completing the traversal, the code returns the list containing the inorder traversal result.
public static IList<int> MorrisTraversalApproach(TreeNode root)
{
// Initialize a list to store the inorder traversal result
List<int> result = new List<int>();
// Initialize the current node pointer to the root of the binary tree
TreeNode curr = root;
// Initialize a pointer to keep track of the predecessor node
TreeNode pre;
// Continue the loop until the current node becomes null
while (curr != null)
{
// If the current node has no left child
if (curr.left == null)
{
// Add the value of the current node to the result list
result.Add(curr.val);
// Move to the next right node
curr = curr.right;
}
else
{
// If the current node has a left subtree
// Find the rightmost node in the left subtree (predecessor node)
pre = curr.left;
while (pre.right != null)
{
// Traverse to the rightmost node
pre = pre.right;
}
// Make the current node the right child of the predecessor node
pre.right = curr;
// Store the current node before moving to its left child
TreeNode temp = curr;
// Move the current node to the top of the new subtree
curr = curr.left;
// Set the left child of the original current node to null
// This prevents infinite loops when traversing the subtree
temp.left = null;
}
}
// Return the list containing the inorder traversal result
return result;
}Postorder Traversal (DFS)
The Postorder Traversal is a tree traversal algorithm used to visit each node in a binary tree systematically. In this approach, you traverse the entire binary tree in the “Left-Right-Root” order.
The nodes are visited in the following order:
- First, visit the Left subtree.
- Then visit the Right subtree.
- Then visit the Root node.
This means that for each node, we first traverse its left subtree, then its right subtree, and finally visit the node itself. In summary, postorder traversal visits the nodes in a bottom-up manner, starting from the leaves and moving towards the root. For example, for the binary three in the image below, the result of the Postorder Traversal is [4, 5, 2, 6, 3, 1]:

Recursive Approach
In the Recursive Approach for postorder traversal, we traverse each node’s left subtree recursively, then traverse its right subtree recursively, and finally visit the current node, resulting in a postorder traversal sequence:
public static IList<int> RecursiveApproach(TreeNode root)
{
List<int> result = new List<int>();
Postorder(root, result);
return result;
}
// Helper method that performs the traversal
private static void Postorder(TreeNode root, List<int> result)
{
if (root == null) return;
// Traverse the left subtree
Postorder(root.left, result);
// Traverse the right subtree
Postorder(root.right, result);
// Visit the current node
result.Add(root.val);
}Iterative Approach using a Stack
In this approach, we start from the root node, we push nodes onto the stack and continue traversal until the stack is empty.
During traversal, we pop nodes from the stack, insert their values at the beginning of the result list to achieve the reverse order of postorder traversal, and then push their right child onto the stack followed by their left child. This ensures that the right subtree is processed before the left subtree, replicating the postorder traversal sequence iteratively.
Note that we insert the value of the current node at the beginning of the result list (result.Insert(0), node.val), and this is done to achieve the reverse order of postorder traversal.
public static IList<int> IterativeApproach(TreeNode root)
{
// Initialize a list to store the result of the postorder traversal
List<int> result = new List<int>();
// Initialize a stack to perform iterative traversal
Stack<TreeNode> stack = new Stack<TreeNode>();
// If the root is null, return the empty result list
if (root == null) return result;
// Push the root node onto the stack to start traversal
stack.Push(root);
// Continue traversal while the stack is not empty
while (stack.Count > 0)
{
// Pop the top node from the stack
TreeNode node = stack.Pop();
// Insert the value of the current node at the beginning of the result list
// This is done to achieve the reverse order of postorder traversal
result.Insert(0, node.val); // Insert at the beginning for postorder traversal
// Push the right child onto the stack first (if exists)
// This ensures that the right subtree is processed before the left subtree
if (node.left != null)
{
stack.Push(node.left);
}
// Push the left child onto the stack (if exists)
if (node.right != null)
{
stack.Push(node.right);
}
}
return result;
}Morris Traversal Approach
In this approach, we start from the root node and we repeatedly traverse the tree until the current node becomes null. During traversal, if the current node has no right child, we process it by adding its value to the output list and moving to its left child. If the current node has a right child, we find its inorder successor, which is the leftmost node of its right subtree. If the successor’s left child is null, we link it to the current node and move to the right child, indicating that we haven’t visited the right subtree yet. If the successor’s left child is not null, we unlink it and move to the left child, indicating that we have already visited the right subtree.
After traversal, we reverse the output list to obtain the postorder traversal sequence.
public static IList<int> MorrisTraversalApproach(TreeNode root)
{
// Create a list to store the postorder traversal result
var output = new List<int>();
// Initialize the current node as the root of the tree
TreeNode node = root;
// Traverse the tree until the current node is not null
while (node != null)
{
if (node.right == null)
{
// If the current node has no right child, process the current node
// Add the value of the current node to the output list
output.Add(node.val);
// Move to the left child of the current node
node = node.left;
}
else
{
// If the current node has a right child
// Find the inorder successor of the current node
TreeNode successor = node.right;
while (successor.left != null && successor.left != node)
{
// Traverse to the leftmost node of the right subtree
successor = successor.left;
}
if (successor.left == null)
{
// If the successor's left child is null, link it to the current node and move to the right child
// This indicates that we haven't visited the right subtree yet
successor.left = node;
// Add the value of the current node to the output list
output.Add(node.val);
// Move to the right child
node = node.right;
}
else
{
// If the successor's left child is not null, unlink it and process the current node
// This indicates that we have already visited the right subtree
successor.left = null;
// Move to the left child
node = node.left;
}
}
}
// Reverse the output to get the postorder traversal
output.Reverse();
// Return the postorder traversal result
return output;
}Level Order Traversal (BFS)
The Level-order traversal traverses the entire tree from Left to Right, level by level. For that, we can use Recursion or use Breadth-First Search (BFS). For example, for the binary three in the image below, the result of the Level Order Traversal is [[1], [2, 3], [4, 5, 6]]:

Recursive Approach
In the Recursive Approach for Level Order traversal, we traverse the entire tree, keeping track of the current level:
public static IList<IList<int>> RecursiveApproach(TreeNode root)
{
// Create a new list to store the result of the level order traversal
IList<IList<int>> result = new List<IList<int>>();
// If the root is null, return an empty list
if (root == null) return result;
// Start the recursive traversal from the root at level 0
LevelOrder(root, 0, result);
// Return the list of levels
return result;
}
// Helper method that performs the traversal
private static void LevelOrder(TreeNode node, int level, IList<IList<int>> result)
{
// If the list of levels doesn't have a list for the current level, create it
if (result.Count == level)
{
result.Add(new List<int>());
}
// Add the current node's value to the appropriate level
result[level].Add(node.val);
// Recursively traverse the left subtree, incrementing the level by 1
if (node.left != null)
{
LevelOrder(node.left, level + 1, result);
}
// Recursively traverse the right subtree, also incrementing the level by 1
if (node.right != null)
{
LevelOrder(node.right, level + 1, result);
}
}Iterative Approach using Breadth First Search (BFS) with a Queue
In this approach, we perform a BFS (which is a technique that is used to traverse or perform searching in data structures like a tree or a graph) on the binary tree, visiting nodes level by level from top to bottom and left to right within each level, and using a queue to manage nodes to be processed at each level:
public static IList<IList<int>> IterativeApproach(TreeNode root)
{
// List to store the result of the level order traversal
var result = new List<IList<int>>();
// If the tree is empty (root is null), return the empty result list
if (root == null)
{
return result;
}
// Queue to manage Breadth-First Search (BFS)
var queue = new Queue<TreeNode>();
queue.Enqueue(root); // Start by enqueuing the root node
// Loop to process nodes at each level
while (queue.Count > 0) // While there are nodes to process
{
// Get the current level size (number of nodes at this level)
int levelSize = queue.Count;
// Create a list to store the node values for the current level
var currentLevel = new List<int>();
// Process all nodes in the current level
for (int i = 0; i < levelSize; i++)
{
// Dequeue the next node from the front of the queue
var currentNode = queue.Dequeue();
currentLevel.Add(currentNode.val); // Add its value to the current level
// Enqueue the left child if it exists
if (currentNode.left != null)
{
queue.Enqueue(currentNode.left);
}
// Enqueue the right child if it exists
if (currentNode.right != null)
{
queue.Enqueue(currentNode.right);
}
}
// Add the current level's node values to the result list
result.Add(currentLevel);
}
// Return the complete level order traversal as a list of lists
return result;
}Reverse Level Order Traversal (BFS)
This approach traverses the entity binary tree from leaf to root (from bottom to top) and from left to right at each level. To achieve this, we can use Recursion or perform a standard level order traversal (using a BFS approach with a queue), but store the results in reverse order, either by collecting levels and then reversing at the end, or by pushing each level’s result to the front of a list (the latter is more efficient, avoiding a full reversal operation at the end).
For example, for the binary three in the image below, the result of the Reverse Level Order Traversal is [[4, 5, 6], [2, 3], [1]]:

Recursive Approach
In the Recursive Approach for Reverse Level Order traversal, we traverse the entire tree from bottom to bottom, from left to right at each level:
// The main function to perform the Reverse Level Order Traversal
public static IList<IList<int>> RecursiveApproach(TreeNode root)
{
// List to store the levels of the tree
IList<IList<int>> levels = new List<IList<int>>();
// Call the recursive helper function to populate the levels
ReverseLevelOrder(root, 0, levels);
// Create a new list to store the reversed levels
IList<IList<int>> reversedLevels = new List<IList<int>>();
// Reverse the order of the levels to achieve bottom-up traversal
for (int i = levels.Count - 1; i >= 0; i--)
{
reversedLevels.Add(levels[i]);
}
// Return the reversed levels as the result
return reversedLevels;
}
// Helper method that performs the traversal
private static void ReverseLevelOrder(TreeNode node, int level, IList<IList<int>> levels)
{
// If the node is null, return (base case)
if (node == null) return;
// If there is no list for the current level, create one
if (levels.Count <= level)
{
levels.Add(new List<int>());
}
// Add the current node's value to the list for this level
levels[level].Add(node.val);
// Recursively traverse the left subtree, incrementing the level by 1
ReverseLevelOrder(node.left, level + 1, levels);
// Recursively traverse the right subtree, incrementing the level by 1
ReverseLevelOrder(node.right, level + 1, levels);
}Iterative Approach using Breadth First Search (BFS) with a Queue
In this approach, we perform a BFS with a queue to traverse the tree level by level, then reverses the order of the levels to create the bottom-up result:
public static IList<IList<int>> IterativeApproach(TreeNode root)
{
// List to store the levels of the tree
IList<IList<int>> levels = new List<IList<int>>();
if (root == null) return levels; // If the tree is empty, return empty list
// Queue to perform BFS
Queue<TreeNode> queue = new Queue<TreeNode>();
queue.Enqueue(root); // Start with the root node
// Traverse the tree level by level
while (queue.Count > 0)
{
// Get the size of the current level
int levelSize = queue.Count;
List<int> currentLevel = new List<int>();
// Process all nodes in the current level
for (int i = 0; i < levelSize; i++)
{
// Dequeue the first node
TreeNode currentNode = queue.Dequeue();
// Add its value to the current level
currentLevel.Add(currentNode.val);
// Enqueue the left child if it exists
if (currentNode.left != null)
{
queue.Enqueue(currentNode.left);
}
// Enqueue the right child if it exists
if (currentNode.right != null)
{
queue.Enqueue(currentNode.right);
}
}
// Add the current level to the levels list
levels.Add(currentLevel);
}
// Reverse the levels to achieve bottom-up order
IList<IList<int>> reversedLevels = new List<IList<int>>();
for (int i = levels.Count - 1; i >= 0; i--)
{
reversedLevels.Add(levels[i]);
}
// Return the reversed levels as the result
return reversedLevels;
}Conclusion
Understanding Binary Trees is fundamental in computer science and serves as a base for various algorithms and data structures. Through this article, we’ve explored key concepts such as nodes, root, parent, child, leaf nodes, and binary tree traversal techniques that use DFS such as Preorder, Inorder, and Postorder traversal, and techniques that use BFS such as Level Order and Reverse Level Order traversal, each offering a unique perspective on the data organization in a binary tree.
This is the link for the project in GitHub: https://github.com/henriquesd/BinaryTreeDemo
If you like this demo, I kindly ask you to give a ⭐️ in the repository.
Thanks for reading!
